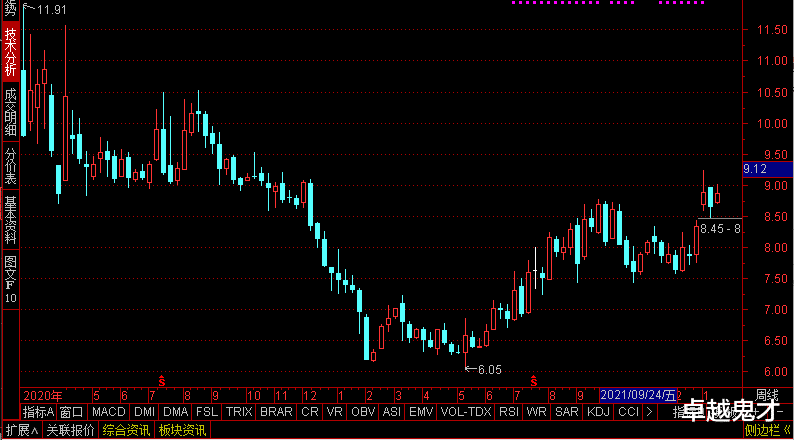
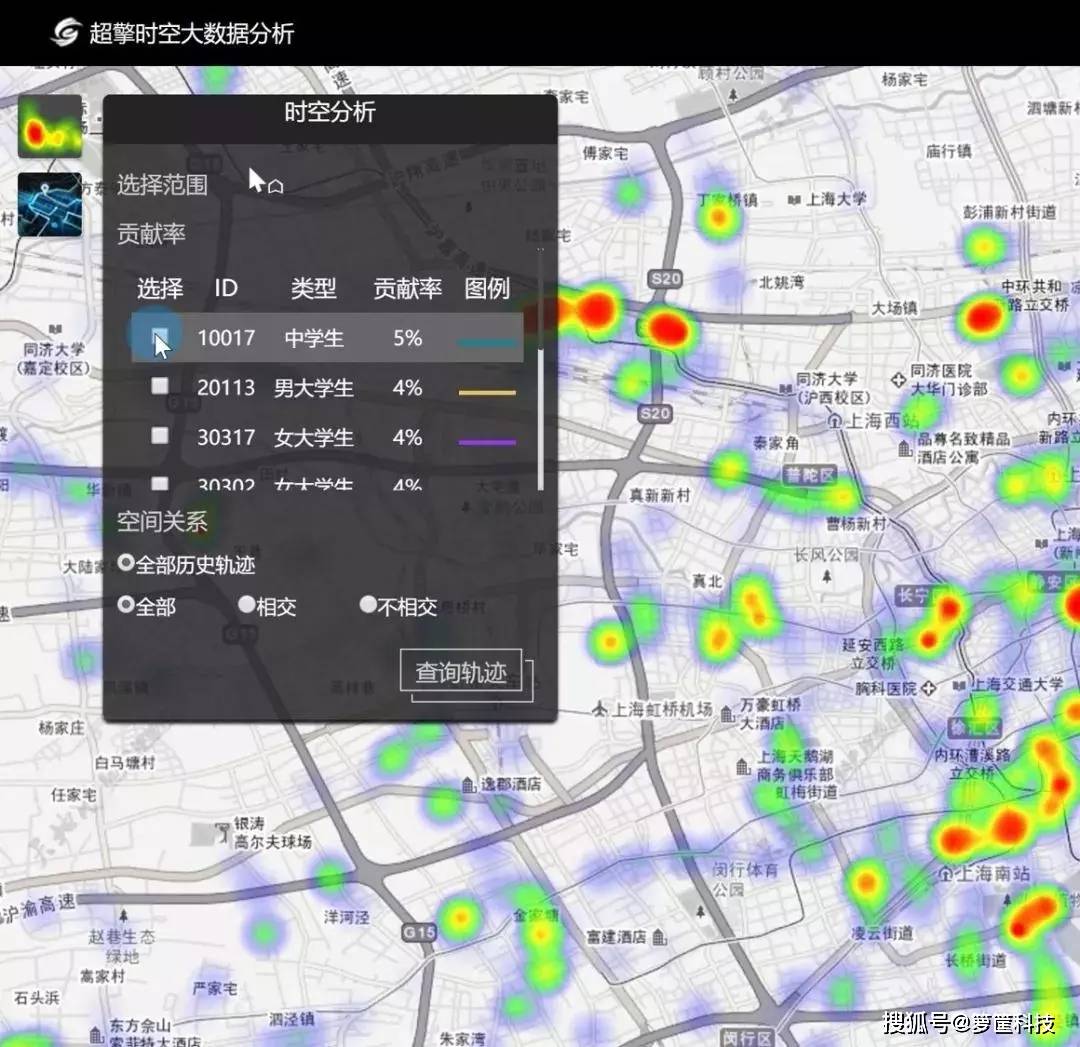
本文探讨了3的最小号走势图，揭示了数字世界中一个奇妙的轨迹。通过分析数学和计算机科学中的算法与模型应用、数据可视化技术以及人类对自然数序列的认知习惯等因素的影响下形成的特定模式或规律性变化趋势，“最”字在“三号”（即第三位）的位置上呈现出一种特殊的排列方式——从左到右依次为1-2（如：0.987654...），而当它被置于首位时则变为最大值形式——“一三五七九”。这种特殊现象不仅反映了人们对数值大小感知上的差异性和复杂性也体现了数字化时代背景下信息处理技术和视觉呈现手段对于人们理解和掌握知识所产生的重要影响作用之一部分内容还涉及到了如何利用这些发现来优化设计界面布局或者提高用户体验等方面问题讨论并给出了相应建议措施等观点论述过程清晰逻辑严密值得读者深入思考和学习借鉴

**引言：从日常到非凡的桥梁——走进数学奇趣》 在浩瀚无垠的知识海洋中，数学的魅力如同夜空中最亮的星，它不仅是科学的基础工具箱、经济决策的关键指标器还是艺术与哲学的灵感源泉。“三”这个看似简单的数字背后隐藏着无尽的奥秘和规律性，“最小的号”——一个既抽象又具象的概念被赋予了新的生命力和解读空间时便成为了我们今天探讨的主题——“‘最小’号的三次元之旅”，本文将通过解析三个维度上的变化趋势来揭示这一概念如何以图形的方式展现其独特的美学价值和应用潜力。《一维视角下的初探“0-1之间的小小步伐》：首先让我们把目光投向最简单的线性世界即一条直线代表的一度量尺上（或称为一轴）。“2.95”（略大于但接近于'∅', 即空集）可以被视为一种特殊情况因为它并不真正存在于实线上而是一个理论极限值；然而当我们将注意力转向更具体且实际存在的数值如"..."等逐渐逼近但又始终小于 '...'" 的序列时就进入了一个微妙而又充满挑战的新领域。"这些点虽然数量无限多却无法构成连续线段因为它们各自独立互不连接形成了一种离散状态下独特的渐变美." 在此背景下 "第n个比前一个大一点点的那个元素"，如果存在的话则构成了该区间内所有可能值的缩影并映射出了一类特殊的函数特征: 单调递增但不完全覆盖整个范围只聚焦在最前端极小的那部分区域.**二、《二维平面的延展："圈外之环"- 从点到面">接着让我们的视野扩展至平面几何的世界里去寻找答案吧！想象一下在一个半径为r圆之外画出一系列同心椭圆其中每个椭圆的中心都位于原定位置不变但其长半軸长度随距离增加逐步减小直至达到某个临界条件后停止增长形成一个类似玫瑰花形状的结构这就是我们所谈论的在特定条件下产生出来具有某种特性的曲线集合之一员-"环形结构". 当我们把焦点放在这组曲线的起始端附近时会发现那里正是那些满足一定规则(例如每一步增量足够小时)所形成的路径开始之处也即是本篇文章主角--"第三种形态": 它虽未直接占据任何完整圆形面积但却以其独有的方式定义了自己在整个系统中的地位.* **《三维空间的跃迁:"螺旋上升"--时间+位置的交响乐章"* 最后也是最为复杂的是当我们引入第三个坐标系--高度/深度之后事情变得更加有趣起来! 现在考虑这样一个场景 : 一条沿着x,y两方向同时旋转同时又沿z向缓慢移动着的螺紡形线路 (这里假设是右旋). 随着这条路径不断延伸下去每一个交叉点和转折处都会记录下一个新数据而这些数据的累积就形成了我们在研究中所说的³´_min'' 或简称为#8467; 最少 #\uFFFD;' 号走勢圖'. 这种模式不仅展示了动态平衡之美还隐含了对自然界及人类社会现象深刻洞察的可能性比如经济学里的泡沫周期论或是生物学细胞分裂过程中DNA复制精确控制等等都是这种思想在不同领域的体现.《总结篇**:超越视觉的艺术 -- 对未来思考的影响*" 通过上述三种不同层次的剖析我们可以看到无论是简单直白的一次方关系亦或者错综复杂的立体模型\"３＇s min＂作为核心要素贯穿其间成为理解事物发展演变过程不可或缺的一部分．它在帮助人们建立更加精准预测能力方面发挥着重要作用同时也激发了我们对于未知领城无尽的好厅心和对知识边界勇敢跨越的精神动力.. 因此无论是在学术研究中还是在日常生活应用中都应重视对这类问题深入探究的价值所在......